Scientific journal

Scientific Review. Chemical sciences

Введение. Исходя из принципа плотной упа­ковки атомов в кристаллах [1], теоретически несложно рассчитать плотность простого вещества, зная основные характеристики его атомов и представляя их в виде упругих сфер. На первый взгляд в этом нет практического смысла, поскольку в зависимости от условий кристаллиза­ции вещество может существовать в различных кристаллических формах, плотность которых не­одинакова [2, 3]. К тому же, понятие атомного радиуса, величина которого лежит в основе расчета, является весьма неопределенным. Эти соображения позво­ляют заключить, что рассчитанная таким образом плотность вещества может значительно отличаться от экспериментальной. Разумеется, может быть вве­ден поправочный коэффициент К: ρэ = Кρр. Однако это имеет смысл только в том случае, если К является величиной постоянной для всех простых веществ или хотя бы для какой-либо группы веществ, на что трудно рассчитывать.

Приведенные доводы являются, по-видимому, одной из причин отсутствия интереса к проблеме корреляции значений плотности веществ, рассчи­танных исходя из геометрических характеристик их атомов и полученных экспериментально. В то же время известно, что для большинства металлов реа­лизуются структуры плотнейших или близких к плотнейшим упаковок, которые характеризуются примерно одинаковой степенью заполнения атома­ми объема кристаллической решетки [4]. Атомы в кристаллических решетках металлов связаны ме­жду собой химическими связями одинаковой при­роды, что обусловливает однотипный характер экс­периментального определения их атомных радиусов и получение при этом сравнимых результатов. Это дает основание предположить, что для металлов ко­эффициент К при определенных условиях может приближаться к некоторому постоянному значению.

Цель исследования. Целью данной работы является обоснование предложенной методики расчета атомных радиусов металлов и других простых веществ и их соединений, обладающих плотнейшей или близкой к ней упаковкой атомов.

Материал и методы исследования. Результаты работы получены обработкой экспериментальных данных о плотности и атомных радиусах металлов, приведенных в литературных источниках, представленных в списке литературы.

Обсуждение результатов. Для всех металлов, для которых известны величины атомных радиусов, было рассчитано соотношение:

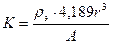(1).

Здесь А – масса атома металла в атомных единицах массы, 4,189r3 – объем атома, представленного в виде сферы радиуса r. Использованные в расчетах значения плотно­сти (в кг/м3) и атомного радиуса (в нанометрах) взяты из работ [5, 6]. Полу­ченные результаты приведены в табл. 1. Их анализ показывает, что большинство значений К находится в пределах 1,16 – 1,26. Более существенные отклоне­ния наблюдаются только для металлов в жидком агрегатном состоянии при комнатной температуре (Hg, Ga), металлов, кристаллическая структура ко­торых не характеризуется плотнейшей упаковкой (Sn, Ge, Po, Sb) и некоторых радиоактивных метал­лов (Pu, Am), определение плотности и атомных ра­диусов которых представляет существенные труд­ности. Коэффициент К связан с плотностью упаков­ки атомов и возрастает при ее увеличении. Это под­тверждается тем, что среднее значение К практиче­ски одинаково для структур типа А1 и A3, имеющих плотнейшую упаковку (74,1%) и составляет, соответ­ственно, 1,224 и 1,227. Для структур типа А2, плот­ность упаковки которых ниже (68%), среднее значе­ние меньше - 1,204. Еще меньшее значение К ~ 0,8 наблюдается для структур типа А4, плотность упа­ковки которых составляет 34%.

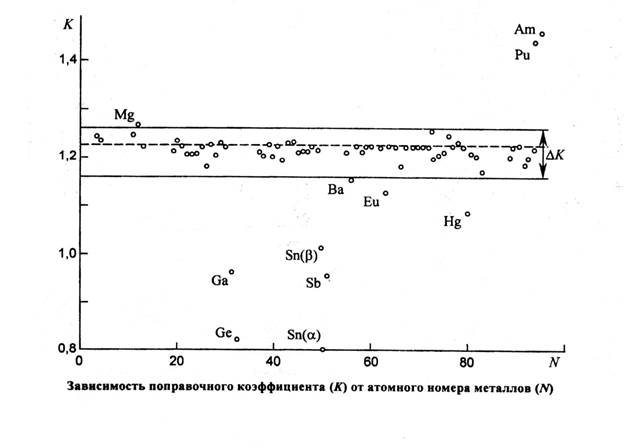
Анализ выборки, представленный на рисунке, свидетельствует, что между величиной К и атомным номером элемента не наблюдается корреляция. Около 90% всех значений К для металлов заключе­но в пределах ΔК = 1,16...1,26. Аппроксимация приведенных на рисунке результатов по методу наименьших квадратов дает значение К = 1,225 (из рассмотрения исключены металлы, значение К для которых выходит за пределы 1,1—1,3). Используя полученное значение К из соотношения (1), можно вывести простые формулы (2) и (3), расчет по кото­рым атомного радиуса и плотности более удобен, чем приведенный в [7] метод расчета через число Авогадро и мольный объем:

r = 0, 664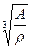; (2) ρ = 0,2924 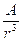, (3)

единицы измерения те же, что в формуле (1).

В табл. 2 приведены расчетные значения атом­ных радиусов металлов, полученные по формуле (2) в сравнении с экспериментально определенными значениями атомных радиусов, которые приведены в работах [5—7]. Анализ данных табл. 2 показывает, что отличие расчетных значений атомных радиусов от экспериментальных в абсолютном большинстве случаев не превышает различия между значениями атомных радиусов одного и того же металла, приведенных в используемых литературных источниках. Более того, средняя величина относительной ошиб­ки расчетных значений атомных радиусов металлов по отношению к экспериментальным результатам (1,314%), рассчитанная по формуле:

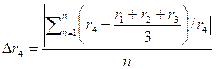, (4)

где величины r1, r2 и r3 — экспериментальные значе­ния атомного радиуса (взяты из работ [2], [6], [5]); r4 – расчетное значение атомного радиуса, оказалась меньшим по сравнению с относительной ошибкой экс­периментальных значений радиусов для каждого из трех используемых литературных источников по от­ношению к двум остальным (5,160%, 2,375%, и 1,507% для источников [5], [6] и [7] соответственно).

Таблица 1. Значения К для металлов

Элемент	Атомный номер	К		Структура [5}
Li	3	1,247		А2
Be	4	1,240		A3
Na	11	1,252		А2
Mg	12	1,273		A3
AI	13	1,225		А1
К	19	1,214		А2
Ca	20	1,238		А1
Sc	21	1,228		A3
Ti	22	1,211		A3
V	23	1,209		А2
Cr	24	1,214		А2
Mn	25	1,227		А1
Fe	26	1,181		А2
Co	27	1,236		A3
Ni	28	1,211		А1
Cu	29	1,239		А1
Zn	30	1,227		A3
Ga	31	0,962		Р
Ge	32	0,825		А4
Rb	37	1,216		А2
Sr	38	1,207		А1
Y	39	1,230		A3
Zr	40	1,201		A3
Nb	41	1,227		А2
Mo	42	1,198		А2
Tc	43	1,236		A3
Ru	44	1,238		A3
Rh	45	1,215		А1
Pd	46	1,217		А1
Ag	47	1,218		А1
Cd	48	1,224		A3
In	49	1,220		Т
Sn(α)	50	0,800		А4
Sn(β)	50	1,018		Т
Sb	51	0,961		Тр
Cs	55	1,214		А2
Ba	56	1,152		А2
Элемент	Атомный номер		K		Структура
La	57		1,229		A3
Се	58		1,219		A3
Рг	59		1,229		A3
Nd	60		1,229		A3
Pm	61		-		-
Sm	62		1,230		Тр
Eu	63		1,129		А2
Gd	64		1,229		A3
Tb	65		1,229		A3
Dy	66		1,189		A3
Ho	67		1,230		A3
Er	68		1,231		A3
Tm	69		1,230		A3
Yb	70		1,229		А1
Lu	71		1,230		A3
Hf	72		1,257		A3
Та	73		1,200		А2
W	74		1,207		А2
Re	75		1,216		A3
Os	76		1,250		A3
Ir	77		1,229		А1
Pt	78		1,237		А1
Au	79		1,226		А1
Hg	80		1,095		-
Tl	81		1,214		A3
Pb	82		1,209		А1
Bi	83		1,178		Тр
Po	84		0,669		К
Fr	87		-		-
Ra	88		1,203		А2
Ac	89		1,225		А1
Th	90		1,230		А1
Pa	91		1,185		A3
U	92		1,200		М
Np	93		1,220		Р
Pu	94		1,450		М
Am	95		1,468		A3

Примечание. Все структуры стабильны при комнатной температуре: А1 — гранецентрированная кубическая; А2 — объемноцентрнрованная кубическая; A3 — гексагональная; А4 — алмазоподобная. Сингонии: К — кубическая; Т — тетрагональная; Тр — тригональная; Р — ромбоэдрическая; М — моноклинная. Для металлов с атомными номерами 96-105 расчеты не проведены из-за недостатка данных, входящих в формулу (1).

С помощью формулы (2) были рассчитаны зна­чения атомных радиусов берклия, кюрия и прометия (табл. 2), данные об экспериментально определен­ных значениях атомных радиусов которых отсутствуют. Формула (3) позволила рассчитать плотность франция (rэ = 0,28 нм; ρFr = 2970,35 кг/м3), сведения о которой отсутствуют в приведенных литературных источни­ках, и уточнить плотность радия, которая согласно работе [5] ≈5000 кг/м3, а расчетное значение соста­вило 5092,5 кг/м3.

Известно из работ [4, 5], что структуры плотнейшей упаковки характерны также для кристаллов инертных газов. Это позволило предположить, что расчетные формулы (2) и (3) применимы и в этих случаях. Данные табл. 3 подтверждают это предпо­ложение, за исключением гелия, определение атом­ного радиуса и плотности которого представляет значительные экспериментальные трудности, что делает весьма вероятной возможность ошибки. Рас­четные значения атомных радиусов остальных инертных газов отличаются от экспериментальных [7] не более, чем на 0,004 нм. Экспериментальные значения плотности кристаллов инертных газов, используемые в расче­тах, взяты из работы [8]. С помощью формулы (3) рассчитана плотность твердого радона (ρRn = 4681,69 кг/м3), сведения о которой отсутствуют в литературе.

Полученные зависимости можно использовать также для расчета плотности некоторых сплавов, если входящие в их состав металлы имеют близкие значения атомных радиусов. Так для сплавов типа твердых растворов замещения может быть предло­жена следующая формула для расчета плотности:

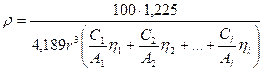. (5)

Таблица 2. Экспериментальные (r1, r2, r3) и расчетные (r4) значения атомного радиуса металлов

Атомный номер	Элемент	r1, нм ×102		r2, нм ×102		r3, нм ×102		r4, нм ×102
3	Li	15,70		15,50		15,20		15,61
4	Be	11,30		11,30		11,13		11,26
11	Na	19,20		18,90		18,58		19,07
12	Mg	16,20		16,00		15,98		16,00
13	Al	14,30		14,30		14,32		14,30
19	К	23,60		23,60		22,72		23,68
20	Ca	19,70		19,70		19,74		19,64
21	Sc	16,40		16,40		16,06		16,39
22	Ti	14,50		14,60		14,48		14,56
23	V	13,40		13,40		13,11		13,46
24	Cr	12,80		12,70		12,49		12,83-12,85*
25	Mn	13,00		13,00		13,66		12,93-13,07*
26	Fe	12,60		12,60		12,41		12,76
27	Co	12,50		12,50		12,53		12,47
28	Ni	12,40		12,40		12,47		12,45
29	Cu	12,80		12,80		12,78		12,76
30	Zn	13,90		13,90		13,32		13,90
31	Ga	13,80		-		12,20		14,50
32	Ge	13,90		-		13,70		15,86
37	Rb	25,30		24,80		24,57		25,37
38	Sr	12,50		21,50		21,52		21,61
39	Y	18,01		18,10		17,76		17,99
40	Zr	15,90		16,00		15,89		16,01
41	Nb	14,70		14,50		14,29		14,70
42	Mo	13,90		13,90		13,63		14,01
43	Tc	13,60		13,60		13,52		13,56
44	Ru	13,40		13,40		13,25		13,36
45	Rh	13,40		13,40		13,45		13,44
46	Pd	13,70		13,70		13,76		13,74
47	Ag	14,40		14,40		14,45		14,43
48	Cd	15,60		15,60		14,89		15,61
49	In	16,60		16,60		16,20		16,63
50	Sn	15,80		-		16,20		16,81-18,21*
51	Sb	16,10		-		14,50		17,46
52	Те	17,00		-		14,30		18,16
55	Cs	27,40		26,80		26,55		27,49
56	Ba	22,10		22,10		21,73		22,54
Атомный номер	Элемент		r1, нм ×102		r2, нм ×102	r3, нм ×102	r4, нм ×102
57	La		18,79		18,70	18,69	18,77
58	Се		18,20		-		18,23-18,33*
59	Pr		18,28		18,20	18,20	18,38
60	Nd		18,21		-	18,14	18,20-18,38*
61	Pm		-		-	-	18,04
62	Sm		18,04		-	-	18,02
63	Eu		19,84		20,20	19,95	20,40
64	Gd		18,01		17,90	17,86	17,99
65	Tb		17,83		17,70	17,63	17,81
66	Dy		17,74		17,70	17,52	17,72
67	Ho		17,66		17,60	14,43	17,64
68	Er		17,57		17,50	17,34	17,55
69	Tm		17,46		17,40	17,24	17,44
70	Yb		19,39		19,30	19,40	19,38
71	Lu		17,35		17,40	17,17	17,33
72	Hf		15,90		15,90	15,64	15,78
73	Та		14,60		14,60	14,30	14,71
74	W		14,00		14,00	13,70	14,08
75	Re		13,70		13,70	13,70	13,74
76	Os		13,60		13,50	13,38	13,51
77	Ir		13,60		13,50	13,58	13,58
78	Pt		13,90		13,80	13,87	13,86
79	Au		14,40		14,40	14,44	14,40
80	Hg		15,70		16,00	15,02	16,31
81	Tl		17,10		17,10	17,04	17,16
82	Pb		17,40		17,50	17,50	17,48
83	Bi		18,20		-	15,43	18,45
84	Po		15,30		-	16,70	18,43-18,72*
88	Ra		23,50		-	-	23,65
89	Ac		20,30		-	18,78	18,76
90	Th		35,90		18,00	17,97	17,96
91	Pa		16,20		16,20	16,06	16,39
92	U		15,30		15,30	13,90	15,41
93	Np		15,00		15,00	13,10	15,03
94	Pu		16,20		-	15,13	16,47
96	Cm		-		-	-	17,49
97	Bk		-		-	-	17,28

Примечание. * – Значения атомного радиуса, полученные при использовании в расчетах двух значений плотности – максимального и минимального

Таблица 3. Экспериментальные (rэ ρэ) и расчетные (rр, ρр) значения атомных радиусов и плотности инертных газов в кристаллическом состоянии

Элемент	rэ, нм ×102 [7]	rр, нм×102	ρэ г/см3 [8]	ρр, г/см3
Не	12,2	17,8	0,194	0,644
Ne	16,0	15,8	1,444	1,441
Аг	19,1	18,8	1,623	1,676
Кг	20,1	20,3	2,826	3,017
Хе	21,8	21,4	3,540	3,706
Rn	22,2		-	4,682

Для основного металла и растворенных метал­лов, радиус атомов которых совпадает с радиусом атомов основного металла η = 1. В табл. 4 приведе­ны результаты расчетов плотности некоторых латуней. Для цинка в расчетах принято значение коэф­фициента η = 1,12. Сравнение полученных данных с экспериментальными свидетельствует о незначи­тельном их различии.

Таблица 4. Экспериментальные (ρэ) и расчетные (ρр) значения плотности некоторых латуней

Марка	Состав, %		ρэ, г/см3 [9]	ρр, г/см3
	Сu	Zn
Л96	96	4	8,85	8,85
Л90	90	10	8,78	8,77
Л85	85	15	8,75	8,75
Л80	80	20	8,66	8,70
Л70	70	30	8,61	8,63
Л68	68	32	8,60	8,60
Л63	63	37	8,40	8,57

Выводы. Полученные результаты могут найти применение в исследованиях атомной структуры ве­ществ, а также позволяют в некоторых случаях уточ­нить экспериментально полученные значения плот­ности металлов и величины их атомных радиусов.

ОБОЗНАЧЕНИЯ

ρэ, ρр – экспериментальная и расчетная плот­ность вещества; А – атомная масса металла; К – поправочный коэффициент; r – атомный радиус ме­талла, кристаллическая решетка которого сохраняет­ся в сплаве (растворитель); С1 С2, ... Сi – концен­трация металлов, входящих в состав сплава; А1, А2, ... Аi – атомные массы металлов; η1, η2,... ηi – попра­вочные коэффициенты, учитывающие искажение кристаллической решетки за счет различия радиусов атомов растворенного металла и растворителя.